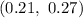Answer:
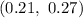
Explanation:
The confidence interval estimate for the population proportion is given by :-
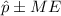 , where
, where
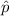 is the sample proportion of success and ME is the margin of error.
is the sample proportion of success and ME is the margin of error.
Given : The proportion of computers that were repaired more than three times in the last two years :
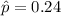
Margin of error :
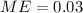
Now, the confidence interval estimate for the population mean will be :-
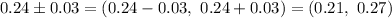
Hence, the 98% confidence interval estimate for the population mean using the Student's t-distribution =