Answer:
The solution to the system of equations is (2,-6).
Explanation:
Given : Equations
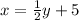 and
and
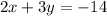
To find : Which ordered pair is the solution to the system of equations?
Solution :
Write the equation
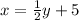 as
as
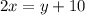 ....(1)
....(1)
Let
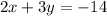 ....(2)
....(2)
Substitute the value of '2x' from (1) in (2),
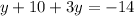
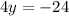
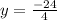
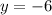
Substitute in
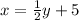 ,
,
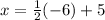
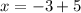

The solution to the system of equations is (2,-6).