Question

The octagon shown below has eight congruent sides. The given measures of the octagon are rounded to the nearest

tenth of a centimeter.
11.6 cm
8.2 cm
28 cm
8.2 cm
- 28 cm
What is the area, to the nearest square centimeter, of the octagon?
A.
392
B. 487
C. 650
D. 720​

Answer 1

Option C
`650\ cm^2`

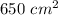
Explanation:

we know that

The area of the octagon can be divided in two trapezoids and one rectangle

so

The area of the octagon is equal to the area of the two trapezoids plus the area of rectangle

step 1

Find the area of one trapezoid

The area of one trapezoid is equal to

`A=(1)/(2)[b1+b2]H`

we have

`b1=28\ cm`

`b2=11.6\ cm`

`H=8.2\ cm`

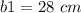
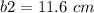
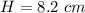
substitute

`A=(1)/(2)[28+11.6]8.2`

`A=162.36\ cm^2`

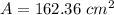
step 2

Find the area of rectangle

The area of rectangle is

`A=bh`

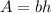
we have

`b=28\ cm`

`h=11.6\ cm`

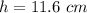
substitute

`A=(28)(11.6)`

`A=324.8\ cm^2`

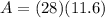
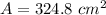
step 3

Find the area of the octagon

`A=(2)162.36+324.8=649.52\ cm^2`

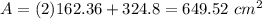
Round to the nearest square centimeter

`649.52=650\ cm^2`