Question

A machine produces open boxes using square sheets of metal. The machine cuts​ equal-sized squares measuring 2 inches on a side from the corners and then shapes the metal into an open box by turning up the sides. If each box must have a volume of 162 cubic​ inches, find the length and width of the open box.

Answer 1

width 9'' length 9''

Explanation:

2 " is cut off from both sides

so the base of the box will be a square

area * height = volume of box

side = x

height =2

2x^2=162

x^2=81

x=9 inches the side of the box

Volume =162

V=area*height V= 81*2= 162

Answer 2

Length is 9 in and width is 9 in.

Explanation:

Suppose the side length of squared shaped sheet of metal is x inches,

∵ After cutting 4 equal squares having side length 2 inches from each corner,

The dimension of the resultant box (x-4) inches ×(x-4) inches × 2 inches,

i.e. length = width = x - 4 inches,

Height = 2 inches,

Tus, the volume of the box,

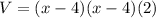`V=(x-4)(x-4)(2)` ( in cubic inches )

According to the question,

`(x-4)(x-4)(2) = 162`

`(x-4)^2 = 81`

`x-4=\pm 9`

`x=13 \text{ or }x = -5`

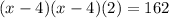
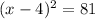
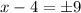
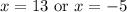
∵ Side can not be negative,

Hence, the length and width of the box = 13 - 4 = 9 inches,