Question

An object has a half-life of 3400 years. The initial amount is 24g. How long until 1 gram remain?

Answer 1

1.56 x 10^4 years

Step-by-step explanation:

Half life, T = 3400 years

initial amount, No = 24 g

Amount remaining, N = 1 g

Let λ be the decay constant.

λ = 0.6931 / T = 0.6931 / 3400 = 2.039 x 10^-4 per year

Let the 1 g amount is remaining in time t.

`N = N_(0)e^(-\lambda t)`

`1 = 24e^{-2.039* 10^(-4)*  t}`

`24= e^{2.039* 10^(-4)*  t}`

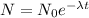
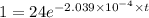
Take log on natural base on both the sides

`3.178= 2.039* 10^(-4)*  t`

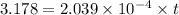
t = 1.56 x 10^4 years