Question

An open metal tank of square base has a volume of 123 m^3

Given that the square base has sides of length x metres, find expressions, in terms of x, for the following.

a)

The height of the tank

b)

The surface area of the tank

c)

Given that the surface area is a minimum, find the value of ????x.

S′(x)=

Therefore,

x= (give your answer to 2 decimal places)

Check this is a minimum.

S″(x)=

Substitute your value for ????x into S″(x) and determine whether is it a minimum.

Type 'Y' for yes, 'N' for no, or 'U' for undefined.

Hence, the minimum area of metal used is

Amin= (give your answer to 2 decimal places)

Answer 1

a) h = 123/x^2

b) S = x^2 +492/x

c) x ≈ 6.27

d) S'' = 6; area is a minimum (Y)

e) Amin ≈ 117.78 m²

Explanation:

a) The volume is given by ...

V = Bh

where B is the area of the base, x^2, and h is the height. Filling in the given volume, and solving for the height, we get:

123 = x^2·h

h = 123/x^2

__

b) The surface area is the sum of the area of the base (x^2) and the lateral area, which is the product of the height and the perimeter of the base.

`S=x^2+Ph=x^2+(4x)(123)/(x^2)\\\\S=x^2+(492)/(x)`

__

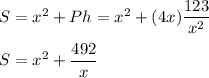
c) The derivative of the area with respect to x is ...

`S'=2x-(492)/(x^2)`

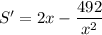
When this is zero, area is at an extreme.

`0=2x -(492)/(x^2)\\\\0=x^3-246\\\\x=\sqrt[3]{246}\approx 6.26583`

__

d) The second derivative is ...

`S''=2+(2\cdot 492)/(x^3)=2+(2\cdot 492)/(246)=6`

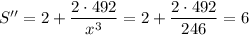
This is positive, so the value of x found represents a minimum of the area function.

__

e) The minimum area is ...

`S=x^2+(2\cdot 246)/(x)=(246^{(1)/(3)})^2+2\frac{246}{246^{(1)/(3)}}=3\cdot 246^{(2)/(3)}\approx 117.78`

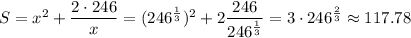
The minimum area of metal used is about 117.78 m².