Question

A vibrating standing wave on a string radiates a sound wave with intensity proportional to the square of the standing-wave amplitude. When a piano key is struck and held down, so that the string continues to vibrate, the sound level decreases by 9.0 dB in 1.0 s. What is the string's damping time constant τ ?

Answer 1

string's damping is 1.03676

Step-by-step explanation:

given data

sound level = 9.0 dB

time = 1 sec

to find out

string's damping

solution

we will apply here formula for string damping (b) that is

A(t) = A ×
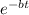`e^(-bt)` ...................1

we know here I ∝ A² so

√I(t) = √I ×
`e^(-bt)`

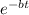
√I(t) / √I =
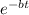`e^(-bt)` .....................2

we know sound level decreases 9 dB i.e ΔdB = 9

so we can write

ΔdB = 10 log ( I(t) / I)

9 = 10 log ( I(t) / I)

I(t) / I =
`10^(-0.9)`

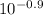
I(t) / I = 0.1258

and

√I(t) / I) = √0.1258 = 0.3546 .......................3

from equation 2 and 3 we get

0.3546 =
`e^(-bt)`

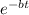
take ln both side

-bt = ln 0.3546

here we know t is 1 sec

so

- b = - 1.03676

b = 1.03676

so here string's damping is 1.03676