Answer:
string's damping is 1.03676
Step-by-step explanation:
given data
sound level = 9.0 dB
time = 1 sec
to find out
string's damping
solution
we will apply here formula for string damping (b) that is
A(t) = A ×
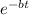 ...................1
...................1
we know here I ∝ A² so
√I(t) = √I ×
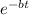
√I(t) / √I =
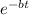 .....................2
.....................2
we know sound level decreases 9 dB i.e ΔdB = 9
so we can write
ΔdB = 10 log ( I(t) / I)
9 = 10 log ( I(t) / I)
I(t) / I =
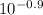
I(t) / I = 0.1258
and
√I(t) / I) = √0.1258 = 0.3546 .......................3
from equation 2 and 3 we get
0.3546 =
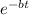
take ln both side
-bt = ln 0.3546
here we know t is 1 sec
so
- b = - 1.03676
b = 1.03676
so here string's damping is 1.03676