Question

One company estimates same day delivery as more than three less than half the total number of miles which graph represents this scenario?

​

Answer 1

The graph D represents this scenario.

Explanation:

We know by reading the exercise that the company estimates same day delivery as a region of the miles.

We can write the same day delivery ''y'' as a region of the miles ''x'' :

`y>(x)/(2) -3`

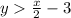
We need to represent this region in a graph.

One way is to find the graph of
`y=(x)/(2)-3`

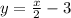
This line will divide the plane into two regions. Then, using any point that verifies the original equation
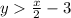`y>(x)/(2)-3` we can find the graph.

Working with the line
`y=(x)/(2)-3` ⇒

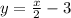If
`x=0` ⇒

`y=(0)/(2)-3\\ y=-3`

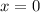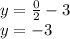
The point
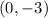`(0,-3)` is the interception of the line with y-axis.

If
`y=0` ⇒
`0=(x)/(2)-3`

`(x)/(2)=3\\ x=6`

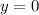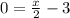
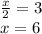
The point
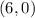`(6,0)` is the interception of the line with x-axis.

We know that
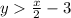`y>(x)/(2)-3` will be the region above of or below of the line
`y=(x)/(2)-3`

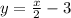
Now using an arbitrary point, for example
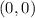`(0,0)` and replacing in the expression :

`0>(0)/(2)-3\\0>-3`

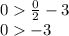
The point
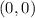`(0,0)` verifies the expression. Therefore, this point belongs to the region.

Finally, we conclude that the region is the region above of the line
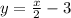`y=(x)/(2)-3` that we can write as
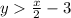`y>(x)/(2)-3` and the correct option is D.

It is important to remark that given the symbol ''>'' and not ''≥'' the line doesn't belong to the region.

Answer 2

Let Same day delivery charge =$ y

If number of miles traveled =x Miles

So,the statement,Same day delivery charge as more than three less than half the total number of miles, in terms of inequality can be Written as

`y>(x)/(2)-3\\\\\rightarrow -y+(x)/(2)>3\\\\-2y+x>6\\\\(x)/(6)+(y)/(-3)>1`

Option D