Question

7. A population of starlings reproduces once per year. The annual geometric growth rate of the population is 4. The population had 80 individuals in 1982. How many individuals will there be in 1984? Assume that starlings die after reproducing, and that individuals mature and can reproduce within a year.

Answer 1

`\boxed{1280}`

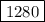
Explanation:

The formula for the nth term of a geometric sequence is

aₙ = a₁rⁿ⁻¹

1. Find the general formula for the sequence

a₁ = 80

r = 4

The general formula is then

aₙ = 80(4)ⁿ⁻¹

Step 2. Find the population in 1984

You want the population at the end of the year.

However, the terms in the sequence represent the population at the beginning of the year

The end of the second year is the beginning of the third year, so you want to evaluate a₃

a₃ = 80(4)³⁻¹ = 80(4)²= 80 × 16 = 1280

`\text{There will be $\boxed{\mathbf{1280}}$ individuals at the end of 1984}`