Answer:

Step-by-step explanation:
The attractive force acting between any tow masses is given by :
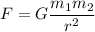
G is the universal gravitational constant
The value of G is,
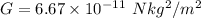
We need to write the value of G in standard notation. A number is written in scientific notation as :
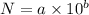
The given value of G is in scientific notation. Its standard notation is given by :

So, the correct option is (d). Hence, this is the required solution.