Question

Consider a 200 g sample of U-238 with decay constant 2.951x10^-16 min^1. Approximately how many disintegrations will occur per minute?

Answer 1

The disintegrations is
`5.902*10^(-17)\ decay /min`.

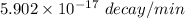Step-by-step explanation:

Given that,

Weight of sample = 200 g

Decay constant
`\lambda=2.951*10^(-16)\ min^(-1)`

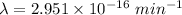
We need to calculate the disintegrations

Using formula of disintegrations

`(dN)/(dt)=\lambda N`

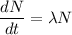
Where,
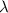`\lambda` = decay constant

N = number of atoms present at time t

Put the value into the formula

`(dN)/(dt)=2.951*10^(-16)*200*10^(-3)`

`(dN)/(dt)=5.902*10^(-17)\ decay /min`

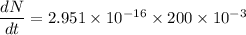
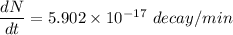
Hence, The disintegrations is
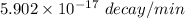`5.902*10^(-17)\ decay /min`.