Answer:
216 degrees is the answer.
Explanation:
The vertical height of the cone = 8 cm
The radius of the cone = 6 cm
The perimeter or circumference of the base of the cone is given by:
P =
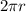
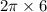 =
=
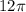
Now the slanted height is calculated using Pythagoras theorem:
H =
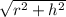
=
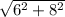
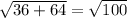 = 10
= 10
Let 'θ' is the sector angle that we have to find.
Arc length of the sector is equal to the perimeter.
Arc length =
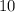 θ
θ
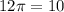 θ
θ
θ=
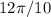
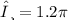 (radian)
(radian)
we know that 1 pi radian = 180 degrees.
So, 1.2 pi radian =
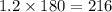 degrees
degrees