Question

A = (1, 3, 5, 7, 9)
B= 2, 4, 6, 8, 10)
C = (1.5.6.7.9)
A U(BOC) =

Answer 1

`A \cup (B \cap C) = (1, 3, 5, 6, 7, 9)`

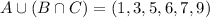
Explanation:

Set A = (1, 3, 5, 7, 9)

Set B = (2, 4, 6, 8, 10)

Set C = (1, 5, 6, 7, 9)

We have to evaluate: A U (B O C) i.e. A union (B intersection C)

First we need to evaluate B intersection C. Remember that intersection of two sets only results in common elements of both the sets. Union of two sets result in all the elements of the two sets combined.

So,

`A \cup (B \cap C) = (1, 3, 5, 7, 9) \cup [(2, 4, 6, 8, 10) \cap (1, 5, 6, 7, 9)]\\\\ A \cup (B \cap C) = (1, 3, 5, 7, 9) \cup (6)\\\\ A \cup (B \cap C) = (1, 3, 5, 6, 7, 9)`