Question

Consider the BVP

y''+(lamda)y=0 y'(0)=0, y'(pi/6)=0

a)assume lamda=0 and find the solution

b)assume lamda>0 and find the solution

c)assume lamda<0 and find the solution

d) Determine the eigenvalues and associated eigenfunctions corresponding the eigenvalues.

Answer 1

`y''+\lambda y=0`

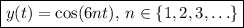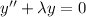
has the corresponding characteristic equation (CE)

`r^2+\lambda=0`

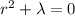
a. If
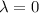`\lambda=0`, then the CE has one root,
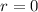`r=0`, and so the general solution to the ODE is

`y(t)=C_1+C_2t`

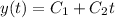
Given that
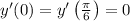`y'(0)=y'\left(\frac\pi6\right)=0`, and

`y'(t)=C_2`

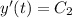
it follows that
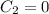`C_2=0`, and so

`\boxed{y(t)=C_1}`

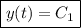
b. If
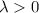`\lambda>0`, then the CE has two complex roots,
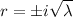`r=\pm i\sqrt\lambda`, and the general solution is

`y(t)=C_1\cos(\lambda t)+C_2\sin(\lambda t)`

`\implies y'(t)=-\lambda C_1\sin(\lambda t)+\lambda C_2\cos(\lambda t)`

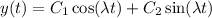
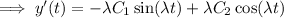
With the given boundary values, we have

`y'(0)=0\implies\lambda C_2=0\implies C_2=0`

`y'\left(\frac\pi6\right)=0\implies-\lambda C_1\sin\left(\frac{\lambda\pi}6\right)=0`

`\implies\sin\left(\frac{\lambda\pi}6\right)=0`

`\implies\frac{\lambda\pi}6=n\pi`

`\implies\lambda=6n`

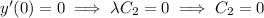
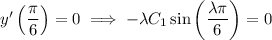
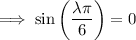
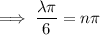
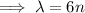
where
`n\in\Bbb Z`.

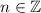• If
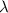  `\lambda` is a (positive) multiple of 6, we have

`y'\left(\frac\pi6\right)=0\implies-6nC_1\sin\left(\frac{6n\pi}6\right)=0\implies C_1=0`

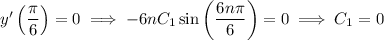
and the solution would be

`\boxed{y(t)=0}`

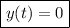
• Otherwise, if
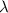  `\lambda` is not a multiple of 6, we have

`y'\left(\frac\pi6\right)=0\implies-\lambda C_1\sin\left(\frac{\lambda\pi}6\right)=0\implies C_1=0`

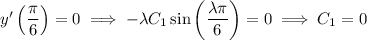
so that we still get

`\boxed{y(t)=0}`

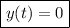
c. If
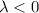`\lambda<0`, then the CE has two real roots,
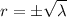`r=\pm\sqrt\lambda`, so that the general solution is

`y(t)=C_1e^(\sqrt\lambda\,t)+C_2e^(-\sqrt\lambda\,t)`

`\implies y'(t)=C_1\sqrt\lambda\,e^(\sqrt\lambda\,t)-C_2\sqrt\lambda\,e^(-\sqrt\lambda\,t)`

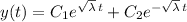
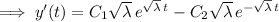
From the boundary conditions we get

`y'(0)=0\implies C_1\sqrt\lambda-C_2\sqrt\lambda=0\implies C_1=C_2`

`y'\left(\frac\pi6\right)=0\implies C_1\sqrt\lambda\,e^((\pi\sqrt\lambda)/6)-C_2\sqrt\lambda\,e^(-(\pi\sqrt\lambda)/6)=0\implies C_1e^((\pi\sqrt\lambda)/3)=C_2`

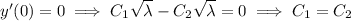
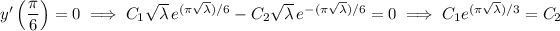
from which it follows that
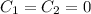`C_1=C_2=0`, so again the solution is

`\boxed{y(t)=0}`

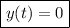
d. We only get eigenvalues in the case when
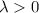`\lambda>0`, as in part (b):

`\boxed{\lambda=6n,\,n\in\{1,2,3,\ldots\}}`

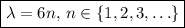
for which we get the corresponding eigenfunctions

`\boxed{y(t)=\cos(6nt),\,n\in\{1,2,3,\ldots\}}`