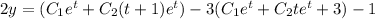Question

Solve the given DE

dx/dt=3x+2y+1

dy/dt=-2x-y+1

Answer 1

We can solve for
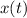`x(t)` first by rewriting the system of first-order ODEs as a single second-order ODE in
`x(t)`:

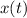Taking the derivative of the first ODE gives

`(\mathrm dx)/(\mathrm dt)=3x+2y+1\implies(\mathrm d^2x)/(\mathrm dt^2)=3(\mathrm dx)/(\mathrm dt)+2(\mathrm dy)/(\mathrm dt)`

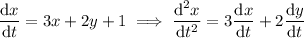
while solving for
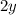`2y` gives

`(\mathrm dx)/(\mathrm dt)=3x+2y+1\implies2y=(\mathrm dx)/(\mathrm dt)-3x-1`

Then

`(\mathrm d^2x)/(\mathrm dt^2)=3(\mathrm dx)/(\mathrm dt)+2(-2x-y+1)`

`(\mathrm d^2x)/(\mathrm dt^2)=3(\mathrm dx)/(\mathrm dt)-4x-2y+2`

`(\mathrm d^2x)/(\mathrm dt^2)=3(\mathrm dx)/(\mathrm dt)-4x-\left((\mathrm dx)/(\mathrm dt)-3x-1\right)+2`

`\implies(\mathrm d^2x)/(\mathrm dt^2)-2(\mathrm dx)/(\mathrm dt)+x=3`

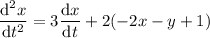
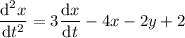
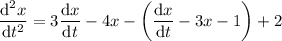
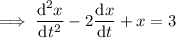
which is linear with constant coefficients, so it's trivial to solve; the corresponding homogeneous ODE

`x''-2x'+x=0`

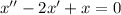
has characteristic equation

`r^2-2r+1=(r-1)^2=0`

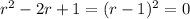
with root
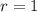`r=1` (multiplicity 2), so the characteristic solution is

`x_c=C_1e^t+C_2te^t`

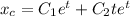
For the non-homogeneous ODE, assume a particular solution of the form

`x_p=a\implies{x_p}'={x_p}''=0`

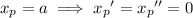
Substituting these into the ODE gives

`0-2\cdot0+a=3\implies a=3`

Then the general solution for
`x(t)` is

`\boxed{x(t)=C_1e^t+C_2te^t+3}`

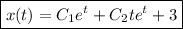
From here, we find

`(\mathrm dx)/(\mathrm dt)=C_1e^t+C_2(t+1)e^t`

so that

`2y=(C_1e^t+C_2(t+1)e^t)-3(C_1e^t+C_2te^t+3)-1`

`\implies\boxed{y(t)=\left(\frac{C_2}2-C_1\right)e^t-C_2te^t-5}`