Question

Mendoza Company's highest point of total cost was $80,000 in June. Their point of lowest cost was $65,000 in January. The company makes a single product. Production volume in June and January were 16,000 and 8,000 units, respectively. What is the fixed cost per month

Answer 1

The fixed costs per month are $50,000.

Step-by-step explanation:

The problem can be presented as a system of 2 equations with 2 variables:

`\left \{ {{80000=y + 16000*x} \atop {65000=y + 8000*x}} \right.`

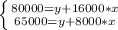
Where:

y are the fixed costs,

x are the variable costs per unit produced.

You can solve the system by the method you like. In this case im using the Gaussian Elimination method.

We start with the following AX = b matrix.

`\left[\begin{array}{ccc}1&16000\\1&8000\\\end{array}\right] * \left[\begin{array}{ccc}y\\x\\\end{array}\right] = \left[\begin{array}{ccc}80000\\65000\end{array}\right]`

We substract the second row by the first row.

`\left[\begin{array}{ccc}1&16000\\0&-8000\\\end{array}\right] = \left[\begin{array}{ccc}80000\\-15000\end{array}\right]`

We divide the second row by (-8000):

`\left[\begin{array}{ccc}1&16000\\0&1\\\end{array}\right] = \left[\begin{array}{ccc}80000\\1.875\end{array}\right]`

We substract the first row by 16,000 times the second:

`\left[\begin{array}{ccc}1&0\\0&1\\\end{array}\right] = \left[\begin{array}{ccc}50000\\1.875\end{array}\right]`

Multiplying this reduced matrix by the X matrix to interpret the results:

`\left[\begin{array}{ccc}1&0\\0&1\\\end{array}\right] * \left[\begin{array}{ccc}y\\x\\\end{array}\right] = \left[\begin{array}{ccc}50000\\1.875\end{array}\right]`

We can say that Mendoza Company's has y = $50,000 fixed costs and each unit costs x = $1.875 to produce. Therefore the answer to the problem is $50,000.