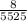Answer:
The probability that the three cards dealt are, in order, an ace, a face card, and a 10 is
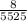
Explanation:
Given : Three cards are dealt from a shuffled standard deck of playing cards.
To find : What is the probability that the three cards dealt are, in order, an ace, a face card, and a 10? (A face card is a jack, queen, or king.)
Solution :
Total number of cards - 52
Number of Ace = 4
Probability of getting an ace is
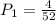
Number of face cards = 12
Probability of getting a face card is
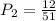
Number of 10's = 4
Probability of getting a 10's is
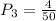
The probability that the three cards dealt are, in order, an ace, a face card, and a 10 is give by
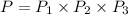
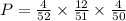
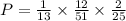
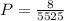
Therefore, The probability that the three cards dealt are, in order, an ace, a face card, and a 10 is