Question

Find the length of an organ pipe closed at one end that produces a fundamental frequency of 256 Hz when air temperature is 18° c A. 0.167 m B.0.334 m C. 0.667 m O D. 1.336 m

Answer 1

B. 0.334 m

Step-by-step explanation:

Given that fundamental frequency of organ pipe which is closed at one end is,
`f_(0)=256Hz`

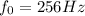
And the temperature of air is,
`T=18^(\circ) C`

Now convert temperature in kelvin,

`T=(18+273)K\\T=291 K`

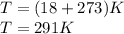
Now the fundamental frequency formula when the organ pipe is open at one end.

`f_(0) =(v)/(2L)`

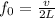
Here, v is the velocity of sound, L is the length of organ pipe.

For further solving it for L.

`L=(v)/(4f_(0) )`

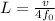
And also we know that,

`v=v_(0)\sqrt{(T)/(273) }`

Here,
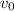`v_(0)` is rthe speed of sound at room temperature and the value of this is,

`v_(0)=331 km/s`.

Now,

`v=331\sqrt{(291)/(273) } \\v=331* 1.0324\\v=341.7373 m/s`

Now put this value in L equation,

`L=(341.7373)/(4* 256) \\L=0.3337 m\\L=0.334 m`

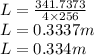
Therefore, the length of an organ pipe is 0.334 m