Question

An electron is located on a pinpoint having a diameter of 3.52 µm. What is the minimum uncertainty in the speed of the electron?

Answer 1

Step-by-step explanation:

It is given that,

An electron is located on a pinpoint having a diameter of 3.52 µm,
`\Delta x=3.52* 10^(-6)\ m`

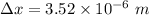
We need to find the minimum uncertainty in the speed of the electron. It can be calculated using Heisenberg uncertainty principal as :

`\Delta p.\Delta x \geq (h)/(4\pi)`

`\Delta p \geq (h)/(4\pi \Delta x)`

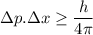
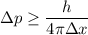
Since, p = m v

So,
`mv \geq (h)/(4\pi \Delta x)`

`\Delta v \geq (h)/(4\pi \Delta x m)`

`\Delta v \geq (6.67* 10^(-34))/(4\pi 3.52* 10^(-6)* 9.1* 10^(-31))`

`\Delta v\geq 16.57\ m/s`

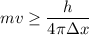
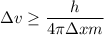
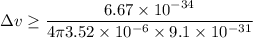
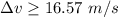
So, the minimum uncertainty in the speed of the electron is greater than 16.57 m/s. Hence, this is the required solution.