Answer:
Thermal energy,
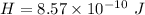
Step-by-step explanation:
It is given that,
Area of loop antenna,
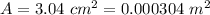
Resistance,
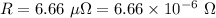
Magnetic field,
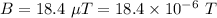
The field magnitude drops to zero in 5.43 ms,
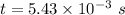
Due to change in magnetic field, an EMF will induced in the loop which is given by :
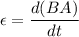
Also,
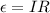
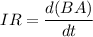
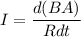
So,
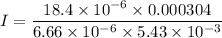
I = 0.154 A
Thermal energy produced is given by,
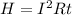
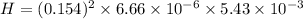
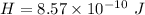
So, the thermal energy produced by changing field is
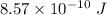 . Hence, this is the required solution.
. Hence, this is the required solution.