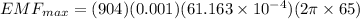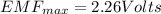Question

A coil of wire (61.163 cm^2 area) can generate a voltage difference when rotated in a magnetic field. If a 904 turn coil is rotated at 65 Hz in a B field of 0.001 T, what is the voltage created ?

Answer 1

`EMF_(max) = 2.26 Volts`

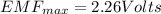
Step-by-step explanation:

As we know that the rotating coil will have change in the angle with time at all instant of time

so at any general instant of time we can say

`\phi = NBA cos\omega t`

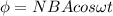
now we have

`EMF = (d\phi)/(dt)`

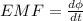
so we have

`EMF = NBA\omega sin\omega t`

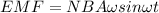
so we have maximum induced EMF in the coil is given as

`EMF_(max) = NBA\omega`

`EMF_(max) = (2\pi f)NBA`

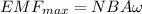
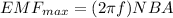
N = 904 turns

B = 0.001 T

`A = 61.163 cm^2 = 61.163 * 10^(-4) m^2`

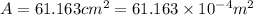
f = 65 Hz

now we have

`EMF_(max) = (904)(0.001)(61.163 * 10^(-4))(2\pi* 65)`

`EMF_(max) = 2.26 Volts`