Question

The emissivity of tungsten is 0.400. A tungsten sphere with a radius of 1.45 cm is suspended within a large evacuated enclosure whose walls are at 320 K. What power input is required to maintain the sphere at a temperature of 3000 K if heat conduction along the supports is negligible?

Answer 1

4850.62 Watt

Step-by-step explanation:

e = 0.4

radius, r = 1.45 cm = 0.0145 m

To = 320 K

T = 3000 k

According to the Stefan's Boltzmann law

Energy radiated per unit time is given by

`E = \sigma Ae\left ( T^(4)-T_(0)^(4) \right )`

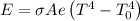
where, σ is the Stefan's constant, A be the area of sphere and e be the emmisivity.

`\sigma = 5.67* 10^(-8) W/m^(2)k^(4)`

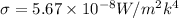
So, Power radiated is energy radiated per second

`E = 5.67*10^(-8)*4*3.14*0.0145*0.0145*0.4*\left ( 3000^(4)-320^(4)\right )`

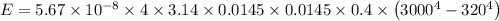
E = 4850.62 Watt