Question

Golden Eagle invests 60% of their funds in stock I and the balance in stock J. The standard deviation of returns on I is 10%, and on J it is 20%. Calculate the variance of portfolio returns, assuming The correlation between the returns is 1.0 The correlation is .5. The correlation is 0.

Answer 1

Variance of the portfolio = 1.96% for Correlation 1.0

Variance of the portfolio = 1.48% for Correlation 0.5

Variance of the portfolio = 1.00% for Correlation 0.0

Step-by-step explanation:

Data Given:

Investment = 60% in stock I and the balance in ( 40% in stock J) = weights

Standard deviation on returns on I = 10%

Standard deviation on returns on J = 20%

Required:

Variance of portfolio returns.

Assumptions:

1) The correlation between returns is 1.0

2) The correlation is 0.5

3) The correlation is 0.0

Solution:σLet's suppose,

Weight of Stock I = w1

Weight of the Stock J = w2

so,

w1 = 60%

w2 = 40%

C = Correlation

SD = Standard deviation

SD1 = SD of stock I

SD2 = SD of stock J

So, the formula for the variance of the portfolio will be:

Variance of the portfolio =
`w1^(2)` .
`SD1^(2)` +
`w2^(2)` .
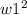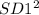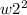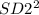`SD2^(2)` + 2(w1.w2.C.SD1.SD2)

Plugging in the values for Assumption 1, where C = 1.0

Variance of the portfolio =
`0.60^(2)` .
`0.10^(2)` +
`0.40^(2)`.
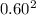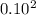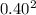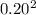`0.20^(2)` + 2(0.60 x 0.40 x 1.0 x 0.10 x 0.20)

Hence,

Variance of the portfolio = 0.0196 x100 to get it in percentage

Variance of the portfolio = 1.96%

Similarly for the assumption 2, where C = 0.5

Variance of the Portfolio =
`w1^(2)` .
`SD1^(2)` +
`w2^(2)` .
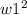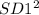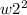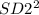`SD2^(2)` + 2(w1.w2.C.SD1.SD2)

Variance of the Portfolio =
`0.60^(2)` .
`0.10^(2)` +
`0.40^(2)`.
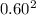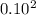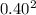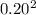`0.20^(2)` + 2(0.60 x 0.40 x 0.5 x 0.10 x 0.20)

Variance of the Portfolio = 0.0148 x 100

Variance of the Portfolio = 1.48%

Similarly, for assumption 3, where C = 0.0

Variance of the Portfolio =
`w1^(2)` .
`SD1^(2)` +
`w2^(2)` .
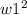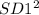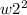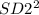`SD2^(2)` + 2(w1.w2.C.SD1.SD2)

Variance of the Portfolio =
`0.60^(2)` .
`0.10^(2)` +
`0.40^(2)`.
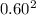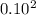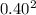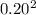`0.20^(2)` + 2(0.60 x 0.40 x 0.0 x 0.10 x 0.20)

Variance of the Portfolio = 0.01 x 100

Variance of the Portfolio = 1%