Answer:
False
Step-by-step explanation:
Let's consider the definition of the angular momentum,
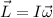
where
 is the moment of inertia for a rigid body. Now, this moment of inertia could change if we change the axis of rotation, because "r" is defined as the distance between the puntual mass and the nearest point on the axis of rotation, but still it's going to have some value. On the other hand,
is the moment of inertia for a rigid body. Now, this moment of inertia could change if we change the axis of rotation, because "r" is defined as the distance between the puntual mass and the nearest point on the axis of rotation, but still it's going to have some value. On the other hand,
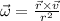 so
so
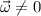 unless
unless
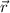 ║
║
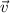 .
.
In conclusion, a rigid body could rotate about certain axis, generating an angular momentum, but if you choose another axis, there could be some parts of the rigid body rotating around the new axis, especially if there is a projection of the old axis in the new one.