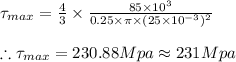Answer:
The correct answer is 231 Mpa i.e option a.
Step-by-step explanation:
using the equation of torsion we Have
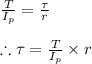
where,
 = shear stress at a distance 'r' from the center
= shear stress at a distance 'r' from the center
T = is the applied torque
 = polar moment of inertia of the section
= polar moment of inertia of the section
r = radial distance from the center
Thus we can see that if a point is located at center i.e r = 0 there will be no shearing stresses at the center due to torque.
We know that in case of a circular section the maximum shearing stresses due to a shear force occurs at the center and equals
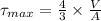
Applying values we get