Question

A storage tank, open at the top, has a diameter 2.60 m and a height 1.80 m . During a storm, the tank catches rain at the rate of 14.8 cm3/s , but water leaks out the bottom through a hole with a cross-sectional area 7.00×10−2 cm2 . Part A What is the maximum depth the water reaches during a long rain storm

Answer 1

The maximum depth of water in the tank shall be 22.784 centimeters.

Step-by-step explanation:

The maximum height will be reached when the rate at which water enters the tank will be equal to the rate at which water will leave the vessel.

Let us assume that the maximum level of water in the tank is 'h' meters

Since the hole is at bottom

According to Torricelli's Law the speed at which the water shall leave the tank equals

`v=√(2gh)`

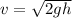
Thus the rate at which water leaves the tank will be equal to

`Q_(out)=Area* Speed`

`Q_(out)=7.00* 10^(-2)* √(2* 981* h)`

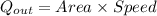
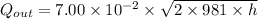
Thus equating the rate of inlet of water and rate of outlet of water we get:

`14.8cm^(3)/s=7.00* 10^(-2)* √(2* 981* h)\\\\\therefore √(h)=(14.8)/(7.00* 10^(-2)* √(2* 981))\\\\\therefore √(h)=4.77\\\\\therefore h=22.784cm`