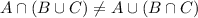Answer:
1.U={1,2,3,4,5}
A={2}
B={2,3}
C={4,5}
2.U={1,2,3,4}
A={1,2}
B={2,3}
C={4}
Explanation:
We are given that
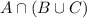 and
and
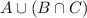
are different sets
1.We have to construct a universe set U and non empty sets A,B and C so that above set in fact the same
Suppose U={1,2,3,4,5}
A={2}
B={2,3}
C={4,5}
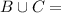 {2,3,4,5}
{2,3,4,5}
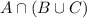 ={2}
={2}
 {2,3,4,5}={2}
{2,3,4,5}={2}
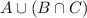 ={2}
={2}
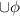 ={2}
={2}
Hence,
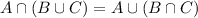
2.We have to construct a universe set U and non empty sets A,B and C so that above sets are in fact different
Suppose U={1,2,3,4}
A={1,2}
B={2,3}
C={4}
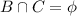
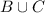 ={2,3,4}
={2,3,4}
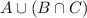 ={1,2}
={1,2}
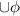 ={1,2}
={1,2}
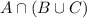 ={1,2}
={1,2}
 {2,3,4}={2}
{2,3,4}={2}
Hence,