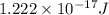Answer: The average kinetic energy of helium atoms is
Step-by-step explanation:
To calculate the average kinetic energy of the atom, we use the equation:
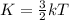
where,
K = average kinetic energy = ?
k = Boltzmann constant =
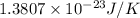
T = temperature =
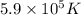
Putting values in above equation, we get:
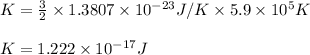
Hence, the average kinetic energy of helium atoms is