Question

12. In a gas mixture consisting of carbon dioxide (CO2) and nitrogen (N2), the carbon dioxide molecules have a root-mean-square speed of 550 m/s. What is the root-mean-square speed of the nitrogen molecules in the sample? CO2 has a molar mass of 44 grams, and N2 has a molar mass of 28 grams. a) 627 m/s b) 752 m/s c) 564 m/s d) 821 m/s e) 689 m/s

Answer 1

The correct answer is option e.

Step-by-step explanation:

The formula used for root mean square speed is:

`\\u_(rms)=\sqrt{(3kN_AT)/(M)}`

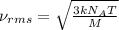
where,

`\\u_(rms)` = root mean square speed

k = Boltzmann’s constant =
`1.38* 10^(-23)J/K`

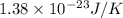
T = temperature

M = Molar mass

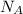`N_A` = Avogadro’s number =
`6.02* 10^(23)mol^(-1)`

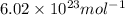
Root mean square speed of carbon dioxide molecule:

`\\u_(rms)= 550 m/s`

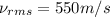
Temperature of the mixture = T =?

Molar mass of carbon dioxide = 44 g/mol = 0.044 kg/mol

`\\u_(rms)=550 m/s=\sqrt{(3* 1.38* 10^(-23)J/K* 6.022* 10^(23)mol^(-1)T)/(0.044 kg/mol)}`

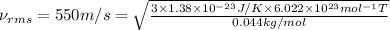
T = 533.87 K

Root mean square speed of nitrogen molecule:

`\\u'_(rms)= ?s`

Molar mass of nitrogen = 28 g/mol = 0.028 kg/mol

`\\u'_(rms)=\sqrt{(3* 1.38* 10^(-23)J/K* 6.022* 10^(23)mol^(-1)* 533.87 K)/(0.028 kg/mol)}`

`\\u'_(rms)=689.46 m/s\approx 689 m/s`

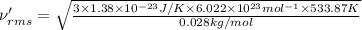
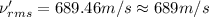
689 m/s is the root-mean-square speed of the nitrogen molecules in the sample.