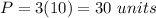Question

In the equilateral triangle XYZ, X is located at (-5, -9) and Z is located at (1, -17). What is the perimeter of Triangle XYZ? a 30 units b 10 units c 25 units d 5 units

Answer 1

Option a. 30 units

Explanation:

we know that

An equilateral triangle has three equal sides

so

XY=YZ=XZ

The perimeter of triangle XYZ is equal to

`P=XY+YZ+XZ`

`P=3XZ`

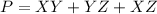
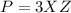
Find the distance XZ

the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

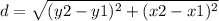
we have

X is located at (-5, -9) and Z is located at (1, -17)

substitute the values in the formula

`XZ=\sqrt{(-17+9)^(2)+(1+5)^(2)}`

`XZ=\sqrt{(-8)^(2)+(6)^(2)}`

`XZ=√(100)`

`XZ=10\ units`

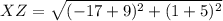
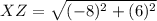
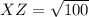
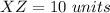
Find the perimeter

`P=3(10)=30\ units`