Answer:
The radius of the toroid is
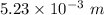 .
.
Step-by-step explanation:
Given that,
Magnetic field B = 2.2 mT
Current =9.6 A
Number of turns = 6.000
We need to calculate the radius
Using formula of magnetic force


Put the value int the formula
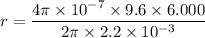
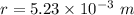
Hence, The radius of the toroid is
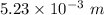 .
.