Question

Solve the following inequality: x^2-8x + 7>0

Answer 1

The solution lie in
`(-\infty,1)\cup(7,\infty)`

Explanation:

Given : Inequality
`x^2-8x+7>0`

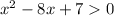
To find : Solve the inequality?

Solution :

First we convert the inequality into equation,

`x^2-8x+7=0`

Solving by middle term split,

`x^2-7x-x+7=0`

`x(x-7)-1(x-7)=0`

`(x-7)(x-1)=0`

`x=7,1`

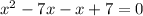
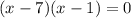
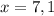
Use each root to create test intervals,

`x<1\\1<x<7\\x>7`

For x<1, let x=0

`0^2-8(0)+7>0`

`0-0+7>0`

`7>0`

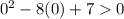
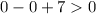
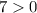
True.

For 1<x<7, let x=3

`3^2-8(3)+7>0`

`9-24+7>0`

`-8>0`

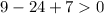
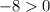
False.

For x>7, let x=8

`8^2-8(8)+7>0`

`64-64+7>0`

`7>0`

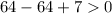
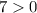
True.

Therefore, The inequality form is x<1 or x>7.

The interval notation is
`(-\infty,1)\cup(7,\infty)`