Question

A recent study conducted by the government attempts to determine proportion of people who support further increase in cigarette taxes. In this study, 2500 voting age citizens were sampled, and it was found that 1900 of them were in favor of an increase in cigarette taxes. Based on the provided data, do you believe that 78% of all citizens are in favor of increasing the tax on cigarette.

Answer 1

Explanation:

Given that recent study conducted by the government attempts to determine proportion of people who support further increase in cigarette taxes.

Sample size = n =2500

Sample persons favouring =1900

Population proportion = 78%

Population std deviation =
`\sqrt{(pq)/(n) } =\sqrt{(0.78*0.22)/(2500) } \\=0.00828`

`H_0: p = 0.78\\H_a: p \\eq 0.78`

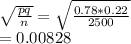
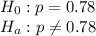
(Two tailed test)

Sample proportion =
`(1900)/(2500) =0.76`

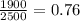
p difference = -0.02

Test statsitic z = p diff / std dev of p

=
`(-0.02)/(0.00828) \\=-2.415`

Since this lies outside 95% of (-1.96, 1.96) we reject H0.

The provided data reveals that the proportion of all citizens are in favor of increasing the tax on cigarette cannot be taken as 78%.