Question

A proton is shot perpendicularly at an infinite plane of charge. The charge density of the plane is +7.65×10^−4 C/m^2. If the proton starts out 1.05 mm from the plane, what must its velocity be so that it screeches to a halt exactly as it reaches the plane?

Answer 1

The velocity is
`2.94*10^(6)\ m/s`.

Step-by-step explanation:

Given that,

Charge density of the plane
`\sigma=7.65*10^(−4)\ C/m^2`

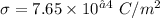
Distance = 1.05 mm

We need to calculate the electric field due to plane of charge

Using formula of electric field

`E=(\sigma)/(2\epsilon)`

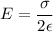
Put the value into the formula

`E=(7.65*10^(−4))/(2*8.85*10^(-12))`

`E=4.322*10^(7)\ N/C`

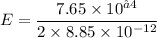
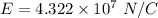
We need to calculate potential difference

Using formula of potential difference

`V=E* r`

Put the value into the formula

`V=4.322*10^(7)*1.05*10^(-3)`

`V=4.5381*10^(4)\ Volt`

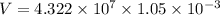
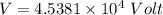
We need to calculate the work requires to be done to reach the surface of the plane

Using formula of work done

`W=qV`

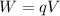
Put the value into the formula

`W = 1.6*10^(-19)*4.5381*10^(4)`

`W=7.26096*10^(-15)\ J`

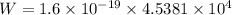
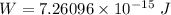
We need to calculate the velocity

Using work energy theorem

`W=(1)/(2)mv^2`

`v^2=(2W)/(m)`

`v=\sqrt{(2*7.26096*10^(-15))/(1.67*10^(-27))}`

`v=2.94*10^(6)\ m/s`

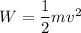
Hence, The velocity is
`2.94*10^(6)\ m/s`.