Question

Find the general solution of

dz/dt=5ze^(sint)cost+2e^(sint)cost

Answer 1

The general solution of given differential equation is
`(1)/(5)ln|5z+2|=e^(\sin t)+C`.

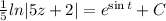Explanation:

The given differential equation is

`(dz)/(dt)=5ze^(\sin t)\cos t+2e^(\sin t)\cos t`

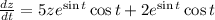
Taking out common factors.

`(dz)/(dt)=(5z+2)e^(\sin t)\cos t`

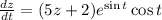
Using variable separable method, we get

`(dz)/(5z+2)=e^(\sin t)\cos t dt`

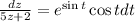
Integrate both sides.

`\int(dz)/(5z+2)=\int e^(\sin t)\cos t dt`

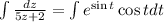
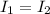`I_1=I_2` .... (1)

First solve LHS,

`I_1=\int(dz)/(5z+2)`

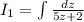
Substitute
`5z+2=u`

`5(dz)/(du)=1`

`dz=(1)/(5)du`

`I_1=(1)/(5)\int(du)/(u)`

`I_1=(1)/(5)ln|u|+C_1`

`I_1=(1)/(5)ln|5z+2|+C_1`

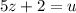
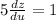
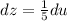
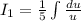
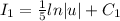
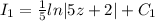
Now, solve RHS,

`I_2=\int e^(\sin t)\cos t dt`

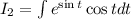
Substitute
`\sin t=v`,

`\cos t(dt)/(dv)=1`

`\cos tdt=dv`

`I_2=\int e^(v)dv`

`I_2=e^(v)+C_2`

`I_2=e^(\sin t)+C_2`

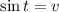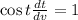
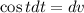
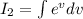
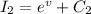
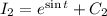
Subtitle the values of I₁ and I₂ in equation (1).

`(1)/(5)ln|5z+2|+C_1=e^(\sin t)+C_2`

`(1)/(5)ln|5z+2|=e^(\sin t)+C_2-C_1`

`(1)/(5)ln|5z+2|=e^(\sin t)+C`

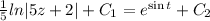
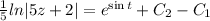
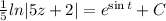
Therefore the general solution of given differential equation is
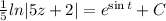`(1)/(5)ln|5z+2|=e^(\sin t)+C`.