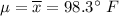Answer with explanation:
The confidence interval for population mean is given by :-
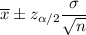
Given : Sample size : n=106
Sample mean :

Standard deviation :
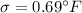
Significance level :
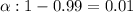
Critical value :
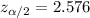
Then , 99% confidence interval estimate of the mean body temperature of all healthy humans will be :-

Since 98.6 is higher than the upper limit of the confidence interval (98.473), then this suggest that the mean body temperature could be lower then 98.6 degrees.
The best estimate of population mean is always the sample mean.