Question

How do you solve this limit of a function math problem? ​

Answer 1

If you know that

`e=\displaystyle\lim_(x\to\pm\infty)\left(1+\frac1x\right)^x`

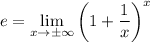
then it's possible to rewrite the given limit so that it resembles the one above. Then the limit itself would be some expression involving
`e`.

For starters, we have

`(3x-1)/(3x+3)=(3x+3-4)/(3x+3)=1-\frac4{3x+3}=1-\frac1{\frac34(x+1)}`

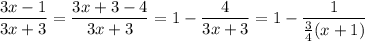
Let
`y=\frac34(x+1)`. Then as
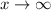`x\to\infty`, we also have
`y\to\infty`, and

`2x-1=2\left(\frac43y-1\right)=\frac83y-2`

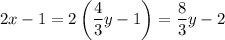
So in terms of
`y`, the limit is equivalent to

`\displaystyle\lim_(y\to\infty)\left(1-\frac1y\right)^(\frac83y-2)`

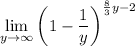
Now use some of the properties of limits: the above is the same as

`\displaystyle\left(\lim_(y\to\infty)\left(1-\frac1y\right)^(-2)\right)\left(\lim_(y\to\infty)\left(1-\frac1y\right)^y\right)^(8/3)`

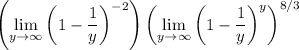
The first limit is trivial;
`\frac1y\to0`, so its value is 1. The second limit comes out to

`\displaystyle\lim_(y\to\infty)\left(1-\frac1y\right)^y=e^(-1)`

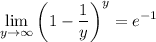
To see why this is the case, replace
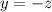`y=-z`, so that
`z\to-\infty` as
`y\to\infty`, and

`\displaystyle\lim_(z\to-\infty)\left(1+\frac1z\right)^(-z)=\frac1{\lim\limits_(z\to-\infty)\left(1+\frac1z\right)^z}=\frac1e`

Then the limit we're talking about has a value of

`\left(e^(-1)\right)^(8/3)=\boxed{e^(-8/3)}`

# # #

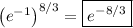
Another way to do this without knowing the definition of
`e` as given above is to take apply exponentials and logarithms, but you need to know about L'Hopital's rule. In particular, write

`\left((3x-1)/(3x+3)\right)^(2x-1)=\exp\left(\ln\left((3x-1)/(3x+3)\right)^(2x-1)\right)=\exp\left((2x-1)\ln(3x-1)/(3x+3)\right)`

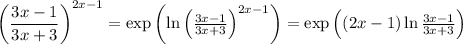
(where the notation means
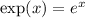`\exp(x)=e^x`, just to get everything on one line).

Recall that

`\displaystyle\lim_(x\to c)f(g(x))=f\left(\lim_(x\to c)g(x)\right)`

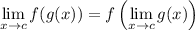
if
`f` is continuous at
`x=c`.
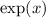`\exp(x)` is continuous everywhere, so we have

`\displaystyle\lim_(x\to\infty)\left((3x-1)/(3x+3)\right)^(2x-1)=\exp\left(\lim_(x\to\infty)(2x-1)\ln(3x-1)/(3x+3)\right)`

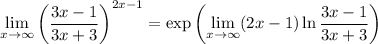
For the remaining limit, write

`\displaystyle\lim_(x\to\infty)(2x-1)\ln(3x-1)/(3x+3)=\lim_(x\to\infty)\frac{\ln(3x-1)/(3x+3)}{\frac1{2x-1}}`

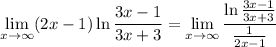
Now as
`x\to\infty`, both the numerator and denominator approach 0, so we can try L'Hopital's rule. If the limit exists, it's equal to

`\displaystyle\lim_(x\to\infty)\frac{(\mathrm d)/(\mathrm dx)\left[\ln(3x-1)/(3x+3)\right]}{(\mathrm d)/(\mathrm dx)\left[\frac1{2x-1}\right]}=\lim_(x\to\infty)\frac{\frac4{(x+1)(3x-1)}}{-\frac2{(2x-1)^2}}=-2\lim_(x\to\infty)((2x-1)^2)/((x+1)(3x-1))=-\frac83`

and our original limit comes out to the same value as before,
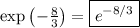`\exp\left(-\frac83\right)=\boxed{e^(-8/3)}`.