Answer:
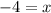
And then we can replace the value of x on equation (1) or (2) and we got:
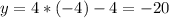
And then we have our solutuon x = -4, y = -20
Explanation:
For this case we have the following system of equations:
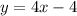 (1)
(1)
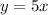 (2)
(2)
And we can solve this system of equation using the method of elimination for example or we can set equal both equation since both are equal to y, like this:
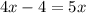
Now w can subtract 4x from both sides and we got:
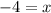
And then we can replace the value of x on equation (1) or (2) and we got:
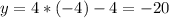
And then we have our solutuon x = -4, y = -20