Question

Assume all telephone numbers are 10 digits long, consisting of a 3-digit area code, then a 3-digit "exchange" number, followed by a 4-digit number. Hovw many telephone numbers have no 0 in the area code and no 9 in the final 4-digit number?

Answer 1

The required answer is:
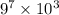`9^7* 10^3` or 4782969000.

Explanation:

Consider the provided information.

All telephone numbers are 10 digits long, consisting of a 3-digit area code, then a 3-digit "exchange" number, followed by a 4-digit number.

The numbers are: 0, 1, 2, 3, 4, 5, 6, 7 ,8, and 9

It is given that no 0 is allow in area code, so for area code we can select 9 numbers out of 10 numbers. i.e 1, 2, 3, 4, 5, 6, 7, 8, and 9

We have 9 numbers for each 3-digit area code,

Area code: 9×9×9 = 9³

no 9 in the final 4-digit number, so for 4-digit code we can select 9 numbers out of 10 numbers. i.e 0, 1, 2, 3, 4, 5, 6, 7, and 8

4-digit number: 9×9×9×9 =
`9^4`

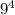
The exchange number can be any number so for exchange number we can select 10 number. i.e 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9

Exchange number: 10×10×10 = 10³

Thus, the total number of possible phone numbers will be:

`9^3* 9^4 * 10^3`

`9^7 * 10^3`

`4782969000`

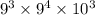
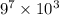
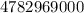
Hence, the required answer is:
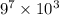`9^7 * 10^3` or 4782969000.