Question

Given that curl F = 2yi – 2zj + 3k, find the surface integral of the normal component of curl F (not F) over (a) the open hemispherical surface x2 + y2 + z2 = 9, z > 0. (b) the sphere x2 + y2 + z2 = 9. (In both parts, you should be able to write the answer down by inspection.)

Answer 1

Use Stokes' theorem for both parts, which equates the surface integral of the curl to the line integral along the surface's boundary.

a. The boundary of the hemisphere is the circle
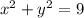`x^2+y^2=9` in the plane
`z=0`, where the curl is
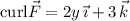`\mathrm{curl}\vec F=2y\,\vec\imath+3\,\vec k`. Green's theorem applies here, so that

`\displaystyle\iint_S\mathrm{curl}\vec F\cdot\mathrm d\vec S=\int_(\partial S)\vec F\cdot\mathrm d\vec r=3\int_(x^2+y^2=9)\mathrm d\vec r`

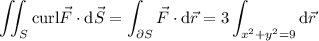
which means the value of the line integral is 3 times the area of the circle, or
`27\pi`.

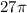b. The closed sphere has no boundary, so by Stokes' theorem the integral is 0.