Question

What is the physical meaning of Schrodinger's wave function? (b). Calculate the minst three energy levels of an electron in an infinite potential well. Consider an electron in an infinite potential well of width 5 Å.

Answer 1

Step-by-step explanation:

(a) The Schrodinger's wave function represent the position of a particle at a particular instant of time. It is also known as the probability amplitude. It is also used to find the location of a particle.

(b) The width of a potential well,
`l=5\ A=5* 10^(10)\ m`

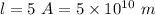
For first energy level, n = 1

Energy in infinite potential well is given by :

`E=(n^2h^2)/(8ml)`

`E=((1)^2* (6.63* 10^(-34))^2)/(8* 9.1* 10^(-31)* 5* 10^(10))`

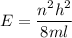
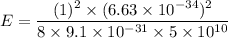
E = 0.0120 Joules

For second energy level, n = 2

`E=(n^2h^2)/(8ml)`

`E=((2)^2* (6.63* 10^(-34))^2)/(8* 9.1* 10^(-31)* 5* 10^(10))`

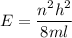
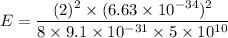
E = 0.0483 Joules

For third energy level, n = 3

`E=(n^2h^2)/(8ml)`

`E=((3)^2* (6.63* 10^(-34))^2)/(8* 9.1* 10^(-31)* 5* 10^(10))`

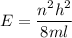
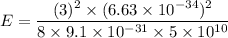
E = 0.108 Joules

Hence, this is the required solution.