Question

In Millikan's oil drop experiment an oil drop is at rest between two large plates separated by 1.3 cm when the potential difference between the plates is 400 V. If the charge carried by the oil drop is that of six electrons, what is the mass of the oil drop?

Answer 1

Mass of the oil drop,
`m=3.01* 10^(-15)\ kg`

Step-by-step explanation:

Potential difference between the plates, V = 400 V

Separation between plates, d = 1.3 cm = 0.013 m

If the charge carried by the oil drop is that of six electrons, we need to find the mass of the oil drop. It can be calculated by equation electric force and the gravitational force as :

`qE=mg`

`m=(qE)/(g)`

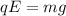
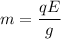
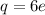`q=6e`, e is the charge on electron

E is the electric field,
`E=(V)/(d)=(400)/(0.013)=30769.23\ V/m`

`m=(6* 1.6* 10^(-19)* 30769.23)/(9.8)`

`m=3.01* 10^(-15)\ kg`

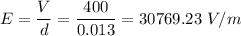
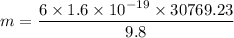
So, the mass of the oil drop is
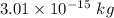`3.01* 10^(-15)\ kg`. Hence, this is the required solution.