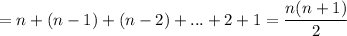Question

Show that the sets of upper-triangular and lower-triangular matrices are subspaces of F n,n . Call them U and L respectively. What are their dimensions?

Answer 1

dim L = dim U =
`(n(n+1))/(2)`

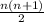
Explanation:

We can do it only for the lower-triangular matrices, the case of the upper-triangular matrices is similar. We might caracterice nxn the lower-triangular matrices, as the nxn matrices
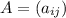`A=(a_(ij))` such that the entry
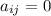`a_(ij)=0` if i<j.

Now let
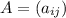`A=(a_(ij))` and
`B=(b_(ij))` be two lower triangular matrices, now if

`C=A+\lambda  B` for some
`\lambda \in \mathbb{F}`

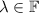
then the entry
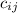`c_(ij)` of C is equal to

`c_(ij)=a_(ij)+\lambda b_(ij)`

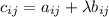
Now, if i<j, it must hold that
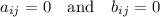`a_(ij)=0 \quad \text{and} \quad b_(ij)=0`. Therefore, if this is the case we must have that
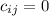`c_(ij)=0` and so we get that C is also a lower triangular matrix. This showa that L is closed under sum and scalar multiplcation, hence it is a linear subspace.

To find the dimension, note that all the entries of a lower-triangular matrix over the diagonal must be equal to zero. However, each entry of the matrix under the diagonal and in the diagonal might be any element of
`\mathbb{F}`, any entry that can be choosen add up to the dimension of L, we n such elemnts for the first column, (n-1) for the second column, (n-2) for the third column etc.... Therefore,

`\dimL=n+(n-1)+(n-2)+...+2+1=(n(n+1))/(2)`