Question

Please help find the formulas for these!! ASAP!!!

Answer 1

`a)\ f(x)=\left\{\begin{array}{cccc}-x+2&for&x\in(0,\ 2]&/0<x\leq2/\\\\-(1)/(3)x+(5)/(3)&for&x\in(2,\ 5]&/2<x\leq5/\end{array}\right`

`b)\ f(x)=\left\{\begin{array}{cccc}-3x-3&for&x\in(-1,\ 0]&/-1<x\leq0/\\\\-2x+3&for&x\in(0,\ 2]&/0<x\leq2/\end{array}\right`

Explanation:

These are graphs of piecewise functions.

Each part is a graph of the linear function.

The slope-intercept form of an equation of a line:

`y=mx+b`

m - slope

b - y-intercept → (0, b)

The formula of a slope:

`m=(y_2-y_1)/(x_2-x_1)`

========================================

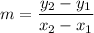
a)

Part 1:

Points (0, 2) → b = 2, and (2, 0).

Calculate the slope:

`m=(0-2)/(2-0)=(-2)/(2)=-1`

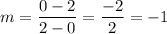
Put the value of m and b to the equation of a line:

`(1)\ y=-1x+2=-x+2`

Part 2:

Points (2, 1) and (5, 0).

Calculate the slope:

`m=(0-1)/(5-2)=(-1)/(3)=-(1)/(3)`

Put the value of the slope and the coordinates of the point (5, 0) to the equation of a line:

`0=-(1)/(3)(5)+b`

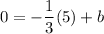
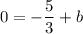`0=-(5)/(3)+b` add 5/3 to both sides

`(5)/(3)=b`

Therefore we have:

`y=-(1)/(3)x+(5)/(3)`

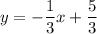
The domain of the function is (0, 2] and (2, 5].

Formula of the piecewise function:

`f(x)=\left\{\begin{array}{cccc}-x+2&for&x\in(0,\ 2]&/0<x\leq2/\\\\-(1)/(3)x+(5)/(3)&for&x\in(2,\ 5]&/2<x\leq5/\end{array}\right`

============================================================

b)

We solve the same as in a) in Part 1

Part 1:

(-1, 0), (0, -3) → b = -3

`m=(-3-0)/(0-(-1))=(-3)/(1)=-3`

`y=-3x-3`

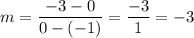
Part 2:

(0, 3) → b = 3, (2, -1)

`m=(-1-3)/(2-0)=(-4)/(2)=-2`

`y=-2x+3`

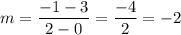
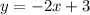
Domain: (-1, 0] and (0, 2].

`f(x)=\left\{\begin{array}{cccc}-3x-3&for&x\in(-1,\ 0]&/-1<x\leq0/\\\\-2x+3&for&x\in(0,\ 2]&/0<x\leq2/\end{array}\right`