Question

In the game of​ roulette, a player can place a ​$66 bet on the number 99 and have a StartFraction 1 Over 38 EndFraction 1 38 probability of winning. If the metal ball lands on 99​, the player gets to keep the ​$66 paid to play the game and the player is awarded an additional ​$210210. ​Otherwise, the player is awarded nothing and the casino takes the​ player's ​$66. Find the expected value​ E(x) to the player for one play of the game. If x is the gain to a player in a game of​ chance, then​ E(x) is usually negative. This value gives the average amount per game the player can expect to lose.

The expected value is $___
The player would expect to lose about $__

Answer 1

The expect value of the game is $ -0.32.

The player is expected to lose about $ 0.32 or 32 cents per game.

Explanation:

Note: The digits in the question statement are pasted twice. Correct values are metal ball lands on 9, player gets to keep his $6, player is awarded $210.

Probability of winning =
`(1)/(38)`

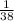
Probability of losing = 1 - Probability of winning

So,

Probability of losing =
`1-(1)/(38)=(37)/(38)`

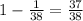
On winning the player gets to keep his $6 and is awarded an additional $210. So, amount of money he will make on winning is $210. On losing the player will lose his $6.

Expected value is calculated as: Sum product of the probabilities with their payouts. The payout on losing will be negative as the money is being lost.

So, expected value of this game would be:

`E(x)=(1)/(38)(210)+(37)/(38)(-6) = -0.32`

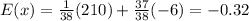
Therefore, the expected value of the game is $ -0.32.

The player is expected to lose about $ 0.32 or 32 cents per game.