Answer: 0.8413
Explanation:
Given : Henry has collected data to find that the typing speeds for the students in a typing class has a normal distribution.
Mean :
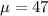
Standard deviation :
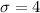
Let x be the random variable that represents the typing speeds for the students.
The z-score :-

For x= 51
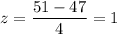
Using the standard normal distribution table ,the probability that a randomly selected student has a typing speed of less than 51 words per minute :-
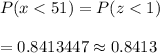
Hence, the probability that a randomly selected student has a typing speed of less than 51 words per minute = 0.8413