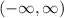Question

F(x)=1/x-2 , g(x)=2x+1/x

A. Use composition to prove whether or not the functions are inverses of each other.
B. Express the domain of the compositions using interval notation.

Answer 1

Yes, they are inverse of each other.

Domain =
`(-\infty, \infty)`

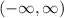
Explanation:

We re given the following:

`f(x) = (1)/(x-2)\\g(x) = (2x+1)/(x)`

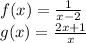
If we calculate the composite function, it will be of the form:

`f(g(x)) = (1)/((2x+1)/(x)-2) \\= (x)/(2x + 1 - 2x)\\= x`

`g(f(x)) = (2((1)/(x-2)) + 1)/(x-2)\\= (2+x-2)/(1)\\\\= x`

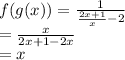
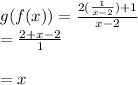
Since, f(g(x)) = g(f((x)) = x, the functions are inverse of each other.

The domain of composite functions, f(g(x)) and g(f((x)) are the values that x can take, so the domain for composite number is all real numbers that is
`(-\infty, \infty)`

Answer 2

A. They are inverses of each other.

Explanation:

A.

If they are inverses of each other then f(g(x)) will be = x.

f(g(x)) = 1 / ( (2x + 1)/ x) - 2)

= 1 / ( 2x + 1 - 2x)/ x

= 1 / 1/x

= x.

So they ARE inverses of each other.