Question

What are the domain and range of the function f(x) = x^4-2x^2-4?

Answer 1

A

Explanation:

Edge

Answer 2

Domain (-∞,∞). Range= f(x) >-5

Explanation:

1) Since we are dealing with a polynomial function with no algebraic restrictions, no denominators, no variables at the exponents, no square roots, etc. And it is a continuous function the Domain is the whole Real Line the Real set of Numbers.

2) As the Range, we have to deal with the combined inverse of this polynomial function.

Do the inversion

`y^4-2x^2-2-x=0`

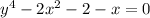
Then susbtitute u²=
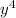`y^(4)` and u=y² back substitute then solve

Jus like this

`u^2-2u-4-x=0`

`u=1+√(x+5)`
`u=1-√(x+5)`

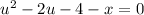
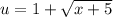
Back substitute and then solve it for y:

y²=x+
`1+√(x+5)`

`y'=\sqrt{1+√(x+5)}\\ y`

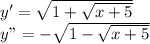
Then y>-5 R=(-5,∞)