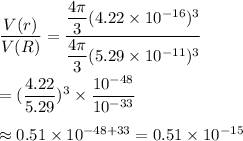Answer:
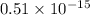
Explanation:
We consider the shape of nucleus and the atom to be sphere.
Also , we know that the Volume of sphere =

Given : Radius of proton :
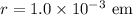
Since 1 em = 0.0042175176 metres
∴
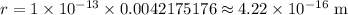
Radius of atom :
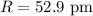
Since,
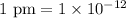
∴Radius of atom :
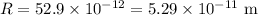
Now, the fraction of the space within the atom is occupied by the nucleus :_